POLINOMIAL ( Suku Banyak )

Assalamu'alaikum Wr.Wb

Dalam dunia pendidikan, matematika adalah pelajaran yang paling ditakuti oleh para pelajar baik siswa/i maupun mahasiswa/i. Padahal, matematika adalah ilmu pasti yang asik dan menarik untuk dipelajari. Dalam kesempatan kali ini, saya Widi Putri kelas XI MIPA dari SMAN 1 Cikalongwetan akan sedikit mengulas tentang Polinomial (suku banyak). Untuk lebih jelasnya mari kita lihat ulasan dibawah ini.

A. POLINOMIAL ( Suku Banyak )

1. Pengertian Polinomial

2x⁵ + 4x⁴ + 8x³ -10x² - 15x + 50

Bentuk Polinomial diatas mempunyai ciri-ciri berikut :

1. Memuat satu variabel yaitu x

2. Pangkat tertinggi atau derajat yaitu 5

3. Koefisien Berturut-turut yaitu 2, 4, 8, -10, dan -15

4. Memiliki Suku tetap atau Konstanta yaitu 50

Dari uraian di atas, dapat diartikan bahwa Polinomial adalah bentuk aljabar yang memuat ciri-ciri sebagai berikut :

- Berpangkat bilangan cacah

- Variabel

- Koefisien

- Operasi matematis

- Konstanta

2. Contoh Polinomial
     
     X⁴+3X³+5X²-7X+15

3. Contoh Bukan Polinomial
 
     X½+2X¾+X-3

4. Operasi Matematis Polinomial
       Operasi matematis Polinomial ada 3, yaitu :
1. Penjumlahan f(x)+g(x)
2. Pengurangan f(x)-g(x)
3. Perkalian f(x)×g(x)

Contoh Soal 

Diketahui suku banyak f(x) dan g(x) sebagai berikut

f(x) = 2x³ - x² + 5x - 10

g(x) = 3x² - 2x + 8

Tentukan :

a) f(x) + g(x)

b) f(x) - g(x)

c) f(x) x g(x)

Penyelesaian

a) f(x) + g(x) = (2x³ - x² + 5x - 10) + (3x² - 2x + 8)

                    = 2x³ - x² + 3x² + 5x - 2x - 10 + 8

                    = 2x³ + 2x² + 3x - 2

b) f(x) + g(x) = (2x³ - x² + 5x - 10) - (3x² - 2x + 8)

                     = 2x³ - x² - 3x² + 5x + 2x - 10 - 8

                     = 2x³ - 4x²  + 7x - 18

c) f(x) x g(x) = (2x³ - x² + 5x - 10) × (3x² - 2x + 8)

              = 2x³(3x² - 2x + 8) - x²(3x² - 2x + 8) + 5x(3x² - 2x + 8) - 10(3x² - 2x + 8)

              = 2x⁵ - 4x⁴ + 16x³ - 3x⁴ + 2x³ - 8x²  + 15x³ - 10x² + 40x - 30x² + 20x - 80

              = 2x⁵ - 7x⁴ + 33x³ - 48x² + 60x - 80

5. Menentukan Nilai Polinomial

        Di dalam menentukan nilai Polinomial, ada dua metode yang dapat digunakan yaitu metode substitusi dan teori Horner.

1. Metode Substitusi

    Metode substitusi yaitu metode dengan mensubstitusi(mengganti) kan nilai x oleh suatu nilai yang ditanyakan.

Contoh soal
Diketahui suku banyak f(x)=2x³ - x² + 5x - 10
Tentukan nilai Polinomial untuk x = 2
Jawab :
 f(x)=2x³ - x² + 5x - 10
 f(2)=2(2)³ - (2)² + 5(2) - 10
 f(2)=16-4+10-10
 f(2)=12

2. Teori Horner

Cara :

- Buat diagram Horner

- Tentukan koefisien tiap variabel

- Tentukan nilai x

- Nilai koefisien pertama ditambah nol, dan hasilnya dikalikan dengan nilai x. Begitu pun seterusnya sampai mendapatkan sisa.

Contoh soal

Diketahui f(x) = X^5+2X⁴+X³-10, dengan nilai x =4.

Jawab :

6. Algoritma Pembagian 

Bentuk Umum :

f(x) = p(x).h(x)+s(x)

Keterangan :

f(x) = bilangan

p(x) = pembagi

h(x) = hasil

s(x) = sisa

1. Cara Bagi Bersusun

2. Teori Horner

7. Teorema Sisa

1. Teorema Sisa I

* Jika suku banyak f(x) dibagi (x-k) maka sisa pembaginya adalah f(x).

Contoh Soal

Tentukan sisa pembagian dari :

f(x) = X³+4X²+6X+2 ÷ (X+2)

2. Teorema Sisa II

* Jika suku banyak f(x) dibagi (ax-b) maka akan bersisa f(b/a)

Contoh soal

Tentukan sisa pembagian dari :

f(x) = X⁴+3X³+2X²+X-5

3. Teorema Sisa III

* Jika suatu suku banyak f(x) ÷ (x-a)(x-b) maka sisanya adalah px+q dimana f(a) = pa+q dan f(b) = fb+q

Contoh Soal

f(x) = x³-2x²+3x-1 ÷ x²+x-2

Penyelesaian :

#memfaktorkan

x²+x-2 = (x+2)(x-1)

a = -2

f(x) = x³-2x²+3x-1 

f(a) = a³-2a²+3a-1

f(-2)=(-2)³-2(-2)²+3(-2)-1

f(-2)= -23

b = 1

f(x) = x³-2x²+3x-1 

f(b) = b³-2b²+3b-1

f(1) =(1)³-2(1)²+3(1)-1

f(1) = 1

f(a) = p(a)+q

f(-2)= p(-2)+q

 -23 = -2p+q

-2p+q = -23 ............(1)

f(b) = p(b)+q

f(1) = p(1)+q

p+q = 1 .................(2)

Metode Eliminasi

-2p+q = -23

   p+q =     1

     -3p= -24

        p= 8

Metode Substitusi

p+q = 1

8+q = 1

     q = 1-8

     q = -7

Maka sisanya adalah px+q = 8x-7.

8. Teorema Faktor 

* Misalkan P (x) = (x - k) H (x) + S maka (x - k) merupakan faktor dari suku banyak P (x) jika dan hanya jika P (k) = 0.

Contoh Soal :

Tunjukan bahwa q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4.

Penyelesaian :

q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4 jika dan hanya jika pembagian 
P (x) oleh q (x) memberikan sisa 0. Mari kita gunakan metode Horner untuk mencari sisa pembagiannya.

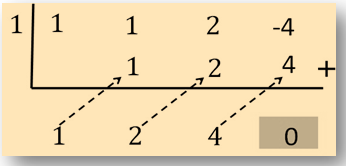
Oleh karena sisa pembagiannya 0, maka q (x) = x - 1 merupakan faktor dari suku banyak 
P (x) = x3 + x2 + 2x - 4.

  Demikian ulasan yang dapat saya uraikan mengenai Polinomial ( suku banyak ). Semoga dapat membantu dan bermanfaat. Sampai jumpa di ulasan berikutnya..

Wassalamu'alaikum Wr. Wb.